Чтож, давайте попробуем рассчитать эффективную процентную ставку своими силами. Для того чтобы осилить это дело потребуется не только вооружиться калькулятором и программой Excel, но и немного наморщить мозг, ибо для рассчета сумм и порядка кредитных платежей нам потребуется освоить некоторые финансовые формулы, которые "для простых смертных" могут показаться не такими уж и очевидными.
Давайте возьмем конкретный пример и рассчитаем его.
Исходные данные:
Аннуитетный платеж означает, что, погашать кредит нужно равными долями в течение всего срока кредитования. Или, попросту говоря, ежемесячно необходимо выплачивать одинаковую сумму. На мой взгляд это наиболее удобный способ погашения кредита.
Для начала - узнаем размер ежемесячного платежа. Для этого нам потребуется формула, приведенная в статье "Аннуитетные платежи".
Напомним, формула выглядит так:
A = K*S, где S - сумма кредита (в нашем случае S = 100 000); K - коэффициент аннуитета, рассчитывается по формуле, зависит от величин i и n.
В данном случае i = 0,015 n = 12. Если мы подставим полученные значения в вышеприведенную формулу, то получим, что
К = 0,09168.
А = $9168.
Способ 2.
Однако, можно сделать немного проще. Для того, чтобы рассчитать размер ежемесячного платежа, воспользуемся встроенной в Excel функцией ПЛТ.
Вводим в ячейку формулу вида:
И получаем ту же сумму: $9168.
Теперь нам нужно составить в Excel'е таблицу ежемесячных платежей:
 |
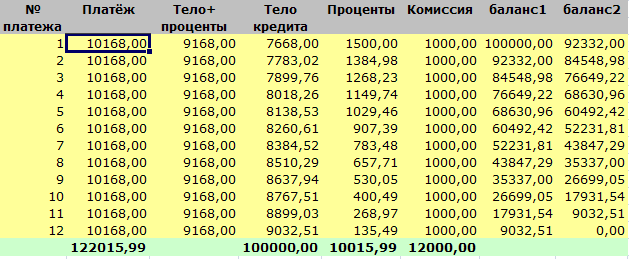| Cкачать таблицу расчёта в формате Excel |
Если вы не до конца поняли, как происходит рассчет - перечитайте статью и смотрите на формулы в строке состояния Excel
Так же обратите внимание, что с каждым месяцем выплаты процентов по кредиту уменьшаются, а выплаты основной части кредита увеличиваются. Это одна из особенностей аннуитетного способа погашения кредита.
Ежемесячная комиссия в 1% обошлась нам в 12000 долларов, что превышает основную сумму выплат по кредиту! Почему так? Потому что комиссию за обслуживание мы каждый месяц платили из рассчета от основной суммы кредита ($100'000), а проценты с каждым месяцем уменьшались ввиду того, что ежемесячно уменьшалась сумма кредита. Как видите, такая, безобидная, на первый взгляд, хитрость банка, как процент за обслуживание при ближайшем рассмотрении обходится очень дорого.
Секрет эффективной процентной ставки сокрыт в указаниях Центробанка РФ № 2008-У «О порядке расчета и доведения до заемщика (физического лица) полной стоимости кредита», датированных 13 мая 2008 года. Оптимальная процентная ставка в виде формулы представлена таким образом:
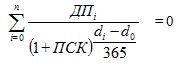
Обозначения символов:
Не менее популярным инструментом для расчета выгодной процентной ставки по версии Центробанка остается программа Excel, в частности ее формула ЧИСТВНДОХ.
Как вы имели возможность убедиться самостоятельно, даже блестящие знания школьного курса математики вряд ли помогут «непосвященным» заемщикам разобраться в сложностях подсчета эффективной процентной ставки. Стоит отметить, что даже если вы осмелитесь наперевес с калькулятором штурмовать финансовые вершины банковских подсчетов, то все равно вряд ли добьетесь нормальных результатов. Все причина в том, что непростая система «скрытых» комиссий наравне со спецификой оборота средств в финансовых учреждениях слишком сложна и непрозрачна, чтобы типичный пользователь мог разобраться в ней самостоятельно.
Так что «розовая» мечта самостоятельно просчитать кредитные ставки и обезопасить себя от чрезмерных выплат для многих плательщиков навсегда останется таковой. Эффективную банковскую ставку, рассчитанную по методике ЦБ, разумно использовать разве что для сравнения аналогичных предложений от разных банков для выбора оптимального вида платежей.
Обычно банки в борьбе за клиентов предлагают невероятно выгодные условия, особенно в отношении кредитов. Многие рекламные материалы строятся на том, что процентные ставки по кредитам именно в этом банке наиболее низкие. Конкретную величину этой ставки, действительно очень привлекательную, часто изображают в качестве одного из основных элементов рекламной композиции буклета или постера. Но почти никто не удосуживается прочитать сносочку где-нибудь внизу или сбоку, которая поясняет, что процентная ставка, - это еще не все и в дополнение к ней существуют всевозможные комиссионные платежи, количество и наименования которых зависят лишь от фантазии банкира. Поэтому будущему клиенту банка очень полезно разобраться, какова же реальная стоимость кредита, то есть рассчитать эффективную процентную ставку (сокращенно - ЭПС).
Очевидно, что из-за нежелания потерять даже малую часть прибыли банки идут на различные уловки и ухищрения. Поэтому объявленная и реальная кредитные процентные ставки могут отличаться отнюдь не на доли процентов и конечно не в пользу клиента.
Величина эффективной процентной ставки позволяет сравнить реальные кредитные условия различных банковских учреждений и провести их объективную оценку.
Если взять в качестве простого примера известную всем кредитную карту, то, рассчитывая ЭПС по ней, следует учитывать комиссии банка - за ведение счета, за обслуживание самой карты и пр. Если банком предлагается льготный кредитный период, то рассчитывать ЭПС необходимо для обоих вариантов - с льготой и без нее. Поскольку поведение заемщика предугадать очень сложно, при расчете ЭПС кредитной карты принимаются такие начальные условия: лимит кредитования и размер задолженности равны, платежи вносятся равными долями, срок кредита - 24 месяца.
В итоге получается, что точную величину ЭПС кредитной карты высчитать можно только приблизительно, в основном из-за непредсказуемости действий заемщика. Но в любом случае эта цифра будет намного больше заявленной банком.
В общем виде расчет эффективной процентной ставки ведется согласно методики, утвержденной в Положении 254-П Центробанка России. При этом обязательно следует учитывать все сборы, проценты и комиссии, уплачиваемые заемщиком банку.
Продолжение статьи:
Формула рассчета Эффективной процентной ставки
Самостоятельный расчет Эффективной процентной ставки
Есть что сказать? Не стесняйтесь!
Последние статьи:
Самый важный закон для должников - закон о банкротстве физических лиц
Подробнее ознакомится с законом о банкротстве физических лиц можно, скачав полный текст закона по ссылке .. 
Нужно ли платить по кредитам?
Путь, как это ни странно, самый выгодный банку и самый сложный для заемщика — договариваться. Но для начала послать пару заказных писем с изложением текущего положения дел. Далее — идем разговаривать, и желательно не с кредитным менеджером, а с его руководителем. Объяснить, что сейчас возможности платить ..
Видео по теме:
УГОЛОК АДМИНИСТРАТОРА